MacKenzie, I. S., & Soukoreff, R. W. (2002). A model of two-thumb text entry. Proceedings of Graphics Interface 2002, pp. 117-124. Toronto: Canadian Information Processing Society. doi:10.20380/GI2002.14. [PDF] [software]
A Model of Two-Thumb Text Entry
I. Scott MacKenzie & R. William Soukoreff
Dept. of Computer ScienceYork University
Toronto, Ontario, Canada M3J 1P3
smackenzie@acm.org, will@acm.org
Abstract
Although text entry has been extensively studied for touch typing on standard keyboards and finger and stylus input on soft keyboards, no such work exists for two-thumb text entry on miniature Qwerty keyboards. In this paper, we propose a model for this mode of text entry. The model provides a behavioural description of the interaction as well as a predicted text entry rate in words per minute. The prediction obtained is 60.74 words per minute. The prediction is based solely on the linguistic and motor components of the task; thus, it is a peak rate for expert text entry. A detailed sensitivity analysis is included to examine the effect of changing the model's components and parameters over a broad range (±50% for the parameters). The model demonstrates reasonable stability - predictions remain within about 10% of the value just cited.
1.1 Introduction
Current research in text entry includes significant interest in the use of small physical keyboards. Some devices allow text entry with as few as five keys, such as the AccessLink II by Glenayre Electronics (Charlotte, NC). Others sport a complete, but miniature, Qwerty keyboard, such as the Blackberry by Research In Motion (Waterloo, Canada). These are both examples of two-way pagers. As well, text entry using the mobile phone keypad has grabbed the attention of users and researchers. While most mobile phones support text entry via the conventional telephone keypad, Nokia has recently introduce the 5510, a mobile phone with a full Qwerty keyboard.Much of the interest is spurred by the remarkable success of so-called SMS messaging on mobile phones (aka text messaging). The ability to discretely, asynchronously, and at very low cost, send a message from one mobile device to another has proven hugely successful, particularly in Europe. The statistics are staggering: Volumes are now approaching 1 billion messages per day! (Various SMS statistics are available at http://gsmworld.com/technology/sms.html) Given the limited capability of the mobile phone keypad for text input, it is not surprising, therefore, that the current wave of mobile text entry research includes numerous researchers and companies working on new ideas to improve text entry techniques for mobile phones or other anticipated mobile products supporting similar services.
In this article, we propose what we believe is the first model of two thumb text entry on small physical keyboards. The model provides both a behavioural description of the interaction plus a predicted peak text entry rate for expert users. In the following sections, the model is described and our prediction is given. This is followed by a detailed analysis examining the model's sensitivity to changes in the various components and parameters that affect the prediction.
Two-thumb text entry is depicted in Figure 1.

Figure 1. Two-thumb text entry
 (b)
(b)
(c)
 (d)
(d)
Figure 2. Devices with miniature Qwerty keyboards (a) Sharp EL-6810 organizer (b) Motorola PageWriter 2000 two-way pager (c) Research In Motion Blackberry two-way pager (d) Nokia 5510 mobile phone
1.2 Model Overview
To model two-thumb text entry, the following steps are proposed:
- Obtain a word-frequency list derived from a language corpus.
- Digitize the miniature keyboard of interest.
- Determine the assignment of the left and right thumbs to letters and keys.
- Given the information in steps 1-3, compute the predicted entry time for each word in the corpus, including the time to enter a terminating
SPACE character after each word.
- Multiply the predicted entry time for each word by the frequency of
the word in the corpus, then sum the values. The result,
tCORPUS , is the time to reproduce the entire corpus.
- Multiply the size of each word (including a terminating a SPACE character)
by the frequency of the word in the corpus, then sum the values. The result,
nCORPUS, is the number of characters in the corpus.
- Compute
tCHAR =
tCORPUS /
nCORPUS . The result,
tCHAR , is the mean time to enter each character in the corpus. The units are
"seconds per character".
- Compute
tWPM = (1 /
tCHAR) × (60 / 5). The result,
tWPM , is the text entry throughput in "words per minute". The scaling
factor includes "second per minute" (60) and "characters per word" (5).
The steps above are similar to those in prior work on text entry on soft keyboards using a stylus [6, 7, 9, 10] and one-finger text entry on a mobile phone keypad [8]. There are two significant departures, however. First, the unit of linguistic analysis is the word. The models in prior work are based on digrams. Second, the motor component of the model works with two thumbs rather than a single finger or stylus. Thus, simple Fitts' law predictions for the time to press a key given a previous key are not possible - at least, in the case where the two keys are pressed by different thumbs.
Each step above is detailed in the following sections.
1.3 Word-Frequency List (Step 1)
Our word-frequency list contains the 9022 most-frequent words in the British National Corpus. It is the same list used by Silfverberg et al. [8] in developing their text entry model for mobile phone keypads. The frequencies total 67,962,112. The shortest word is "a" (frequency = 1,939,617), while the longest word is "telecommunications" (18 letters, frequency = 1221). The average word size is 7.088 characters if a simple mean is calculated, or 4.427 characters if weighted by the word frequency.Although our model's predictions are generated using a word-frequency list, digram-frequency and letter-frequency lists are also useful to facilitate certain analyses, for example, on SPACE key usage and word transitions. Both are easily built from the word-frequency list, with the added assumption that each word is followed by a SPACE. The letter-frequency list has 27 letters (A-Z, SPACE) with frequencies totaling 368,832,032. The digram-frequency list has 27 × 27 = 729 digrams, with frequencies again totaling 368,832,032. Some statistics from these lists are now given.
| Letters | Frequency | % of Letters |
|---|---|---|
| SPACE | 67,962,112 | 18.43% |
| All others | 300,869,920 | 81.57% |
| Total | 368,832,032 | 100.00% |
| Digrams at Start of Word | Frequency | % of Start-of-word Digrams | % of Digrams |
|---|---|---|---|
| SPACE-left | 44,686,347 | 65.75% | 12.12% |
| SPACE-right | 23,275,765 | 34.25% | 6.31% |
| Total | 67,962,112 | 100.00% | 18.43% |
| Digrams at End of Word | Frequency | % of End-of-word Digrams | % of Digrams |
|---|---|---|---|
| left-SPACE | 47,905,787 | 70.49% | 12.99% |
| right-SPACE | 20,056,325 | 29.51% | 5.44% |
| Total | 67,962,112 | 100.00% | 18.43% |
1.4 Digitized Keyboard (Step 2)
Digitizing a keyboard is straight-forward. Working with an image of a keyboard, the x-y coordinate and the size of each key is measured and entered into a table along with the letter assigned to the key. For rectangular or elliptical keys, the smaller of the width and height dimensions is entered as the size of the key, as suggested in prior Fitts' law research [4]. The units are arbitrary. Our measurements were gathered using the pixel coordinates of an image processing application.
We used the Sharp EL-6810 as a representative keyboard for testing our model (see Figure 2a). The digitized rendering is shown in Figure 6.
| Letter | X Position | Y Position | Size |
|---|---|---|---|
| q | 46.0 | 314 | 35 |
| w | 119.4 | 314 | 35 |
| e | 192.8 | 314 | 35 |
| r | 266.2 | 314 | 35 |
| t | 339.6 | 314 | 35 |
| y | 413.0 | 314 | 35 |
| u | 486.4 | 314 | 35 |
| i | 559.8 | 314 | 35 |
| o | 633.2 | 314 | 35 |
| p | 706.6 | 314 | 35 |
| a | 80.0 | 366 | 35 |
| s | 153.4 | 366 | 35 |
| d | 226.8 | 366 | 35 |
| f | 300.2 | 366 | 35 |
| g | 373.6 | 366 | 35 |
| h | 447.0 | 366 | 35 |
| j | 520.4 | 366 | 35 |
| k | 593.8 | 366 | 35 |
| l | 667.2 | 366 | 35 |
| z | 118.0 | 418 | 35 |
| x | 191.4 | 418 | 35 |
| c | 264.8 | 418 | 35 |
| v | 338.2 | 418 | 35 |
| b | 411.6 | 418 | 35 |
| n | 485 | 418 | 35 |
| m | 558.4 | 418 | 35 |
| _ | 416 | 470 | 35 |
(Note: '_' represents the SPACE key)
1.5 Assignment of Thumbs to Letters and Keys (Step 3)
To determine the assignment of thumbs to letters and keys, a few assumptions are necessary. A reasonable assumption is that each thumb presses keys normally pressed by the corresponding hand during touch typing. This is illustrated in Figure 7.

Figure 7. Assumed use of left and right thumbs for two-thumb
text entry on a miniature Qwerty keyboard
Although it is uncertain whether the thumb assignments in Figure 7 occur in practice, this is a reasonable start. Changes are easily introduced later to accommodate different thumb-to-key assignments. Given the assignments in Figure 7, it is known which thumb is used to enter each letter. Figure 8 shows an example, where L is for the left thumb, R is for the right thumb.

Figure 8. Example phrase and thumb assignment for two-thumb text
entry (see text for discussion on SPACE key usage)
1.5.1 SPACE Key Policy
SPACE key usage is problematic, since the size and position of the SPACE key varies among devices. If the SPACE key is centrally located, as with standard keyboards, then it is equally accessible to the right or left thumb. Since SPACEs constitute about 18% of English text entry, it is important to embed in our model an appropriate behavioural description of SPACE key usage. We call this the SPACE Key Policy. The following three SPACE key policies seem tenable.
Alternate Thumb. One possibility is that the SPACE key is activated by the alternate thumb to that used for the last letter in a word. This behaviour is shown for the example phrase in Figure 8. Viewed in isolation, this is optimal. For two-handed touch typing, for example, it is known that keying time is less when the preceding key is pressed by a finger on the opposite hand [3]. Arguably, the first letter in the next word should also be considered; however, this complicates the model and will not be considered at the present time.
Left Thumb. The left thumb SPACE key policy assumes simply that the SPACE key is always pressed by the left thumb.
Right Thumb. With a right-thumb SPACE key policy, the SPACE key is always pressed by the right thumb.
The left-thumb and right-thumb SPACE key policies are particularly appealing if the SPACE key is positioned on either the left or right side or the keyboard, as seen, for example, in Figure 2b and Figure 2d where the SPACE key is on the left. In these cases, the model should likely adopt a left-thumb SPACE key policy.
1.5.2 Thumb Transitions
Given our three SPACE key policies and the earlier assumptions on the assignment of thumbs to letters and keys, it is possible to categorize two-thumb text entry by thumb transitions for each digram in our corpus. This is shown in Figure 9.
 (b)
(b)
 (c)
(c)

Figure 9. Thumb transitions by SPACE key policy (a) alternate thumb (b) left thumb (c) right thumb
The ratios in Figure 9 are of 368,832,032 total frequencies in the digram-frequency list cited above. Among the insights in Figure 9 is the identification of key actions characterized by Fitts' law. These are the key sequences LEFT-LEFT or RIGHT-RIGHT. For the alternate thumb SPACE key policy (Figure 9a), about 36.8% of the actions are of this type, whereas 63.2% of the key actions are of the form LEFT-RIGHT or RIGHT-LEFT. Our method of modeling the key actions and thumb transitions is explained in the next section.
1.6 Predicted Entry Times (Step 4)
Our next step is to determine the predicted entry time for each word in the corpus. Before giving a detailed analysis, we introduce tMIN, the minimum time between keystrokes on alternate thumbs. We use
| tMIN = 1/2 × tREPEAT | (1) |
where tREPEAT is the time to press one key repeatedly with the same finger. The rationale is based on research in two-handed touch typing, as reported in Card et al. [1, p. 60]. The idea is depicted in Figure 10. The time between keystrokes when using one thumb to repeatedly type the same key is tREPEAT (depicted in Figure 10a). When using two thumbs to repeatedly alternate between two keys, the keystroke rate almost doubles because the movement of the two thumbs overlaps (Figure 10b).
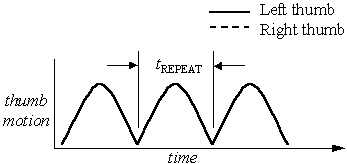
(b)
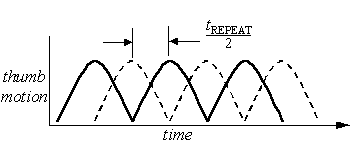
Figure 10. Illustration of key repeat time (a) single thumb (b) alternating thumbs

Figure 11. Computing entry time for a word
We use the values just cited as weighting factors in determining t1. The example word in Figure 11 begins with a left-thumb keystroke. If the left thumb was used for the preceding SPACE, the movement time for first letter is tFITTS, where tFITTS is the time for the left thumb to move to and press the key bearing the first letter in the word, having just pressed the SPACE key. If the right thumb was used for the preceding SPACE, we assume the left thumb is poised to enter the first letter with negligible movement. In this case, movement time is tMIN. We combine these descriptions with the weighting factors to accommodate uncertainty on which interaction takes place. Since the example word in Figure 8 begins with a left-thumb keystroke, we use
| t1 = 0.2951 × tFITTS + 0.7049 × tMIN | (2) |
For words beginning with a right-thumb keystroke, we use the same formula, except the weighting factors are reversed.
Time t2 in Figure 11 is simply
| t2 = t1 + tFITTS | (3) |
where tFITTS, in this case, is the time for the left thumb to move to and acquire the key bearing the second letter, having just entered the first. A similar calculation is used throughout a word if the same thumb is used for the preceding letter.
The third letter in the example is entered with the right thumb. There is again uncertainty on the preceding interaction. For the sequence in Figure 11, we use
| t3 = max(t2 + tMIN, t0 + tFITTS) | (4) |
In this case, tFITTS is the time for the right thumb to press the key bearing the third letter having previously pressed the SPACE key (which occurs at t0 in the example). At the very least, t3 should be t2 + tMIN, so we choose the maximum of these two possibilities. A similar calculation is used throughout a word if a different thumb is used for the preceding letter.
To complete the example,
| t4 = max(t3 + tMIN, t2 + tFITTS) | (5) |
| t5 = max(t4 + tMIN, t3 + tFITTS) | (6) |
| t6 = max(t5 + tMIN, t4 + tFITTS) | (7) |
This completes our example walk-through for the key sequence in Figure 11. Let's re-state the procedure in general terms. For the first letter in a word, we use
| t1 = 0.2951 × tFITTS + 0.7049 × tMIN | (8) |
if entered with the left thumb, or
| t1 = 0.7049 × tFITTS + 0.2951 × tMIN | (9) |
if entered with the right thumb. For subsequent letters, we use
| tn = tn-1 + tFITTS | (10) |
if the same thumb is used for the previous letter, or
| tn = max(tn-1 + tMIN, tRECENT + tFITTS) | (11) |
if the opposite thumb is used for the previous letter. The time stamp of the most recent use of the same thumb is represented by tRECENT, which is at least two keystrokes before the current keystroke. Of the four equations above, equation 11 is used most often (about 57% of the time). It is for this reason – considering more than one preceding keystroke – that our model is based on words rather than digrams.
1.6.1 Model Coefficients
An important component of the model is missing. Fitts' law models have not been reported for pressing keys with thumbs, as shown in Figure 1. Two models are needed: one for the preferred hand, and one for the non-preferred hand. A related model is reported by Silfverberg et al. [8] for the thumb on the preferred hand pressing keys on a mobile phone keypad:
| MT = 176 + 64 × log2(A / W + 1) | (12) |
where A is the amplitude of the movement and W is the width of the destination key. We can tentatively use this model for both thumbs. As well, tREPEAT = 176 ms in Equation 1. So, a tentative value for tMIN is
| tMIN = 88 ms | (13) |
1.7 Model Predictions (Steps 5-8)
With these model coefficients, and the behavioural description above, all the components of the model are in place. A Java program was written to generate a prediction, as per the procedure and coefficients just described. The program works with a SPACE key policy, a word-frequency list and a digitized rendition of a keyboard. Our default invocation uses the alternate thumb SPACE key policy, the 9022 word-frequency list from the British National Corpus, and a digitization of the Sharp EL-6810 keyboard in Figure 2a. Our program provides the following prediction for two-thumb text entry:
| tWPM = 60.74 wpm | (14) |
Previous predictions for key-based mobile text entry are in the range of 20.8 wpm to 45.7 wpm [5, 8]. Although our prediction of 60.74 wpm seems quite high, it is important to remember that it is a peak rate for experts and it is for dual-stream input using two thumbs. Rates of 80 wpm, or beyond, are readily attained by expert touch typists on standard keyboards; so our prediction is not unreasonable.
1.8 Sensitivity Analysis
There are numerous factors influencing our model's prediction. A useful exercise, therefore, is to test the sensitivity of the model to changes in the components and parameters contributing to the prediction. Such an exercise is known as a sensitivity analysis. For examples, see [1, 8].
1.8.1 Slope Coefficient
A good start is to vary the slope coefficient in the Fitts' law model and observe the effect on the model's predictions. As noted earlier, we tentatively used Silfverberg et al.'s [8] model for pressing keys with the thumb, using the same model for both thumbs. The slope coefficient in their model is 64 ms/bit (see Equation 12). Figure 12 illustrates the effect of systematically altering the slope coefficient. For this, we generated six additional predictions: three with higher slope coefficients (+10%, +20%, and +50%) and three with lower slope coefficients (−10%, −20%, and −50%).
| Slope Coefficient (ms/bit) | WPM Prediction | ||
|---|---|---|---|
| Value | % of Nominal | Value | % of Nominal |
| 32.0 | 50% | 76.44 | 125.8% |
| 51.2 | 80% | 66.18 | 109.0% |
| 57.6 | 90% | 63.35 | 104.3% |
| 64.0* | - | 60.74* | - |
| 70.4 | 110% | 58.34 | 96.0% |
| 76.8 | 120% | 56.12 | 92.4% |
| 96.0 | 150% | 50.37 | 82.9% |
| * Nominal values | |||
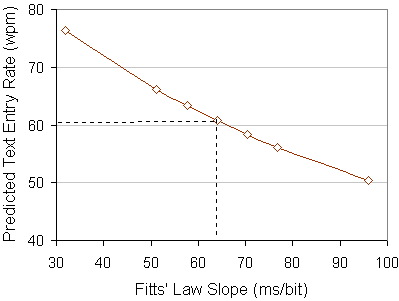
Figure 13. Sensitivity to the Fitts' law slope coefficient,
chart form (dashed line shows nominal value)
1.8.2 tMIN
Our model makes frequent use of tMIN, the assumed minimum time between key presses with alternate thumbs. We nominally set tMIN = 88 ms, or one half the intercept in the Fitts' law equation, as explained earlier. However, it is not clear that users will exhibit such behaviour during normal or high speed text entry. And so, examining the influence of tMIN on the model is worthwhile. Figure 14 shows this influence, replicating the procedure in the preceding section.
| tMIN Coefficient (ms) | WPM Prediction | ||
|---|---|---|---|
| Value | % of Nominal | Value | % of Nominal |
| 44.0 | 50% | 63.84 | 105.1% |
| 70.4 | 80% | 61.97 | 102.0% |
| 79.2 | 90% | 61.36 | 101.0% |
| 88.0* | - | 60.74* | - |
| 96.8 | 110% | 60.12 | 99.0% |
| 105.6 | 120% | 59.51 | 98.0% |
| 132.0 | 150% | 57.47 | 94.6% |
| * Nominal values | |||
1.8.3 Key Widths
As well as sensitivity to the Fitts' law coefficients, our model is sensitive to the assumed width of the keys, which is confounded with the width of the thumb. Our model uses the key heights as W in the model, since key height is the smaller of the width and height dimensions of the keys. This assignment for target width was used by Silfverberg et al. [8] and is recommended in prior Fitts' law research [4]. However, the input "device" is a thumb, not a stylus, so the "effective key width" may be somewhat larger if we also consider the width of the thumb. This was noted by Drury [2] in a study of keying times on calculators with various inter-key gaps. If the assumed key widths are increased by 10%, 20%, and 50%, for example, the word-per-minute prediction increases by 1.9% (61.89 wpm), 3.7% (62.96 wpm), and 8.3% (65.76 wpm), respectively.

Figure 15. Sensitivity to tMIN, chart form (dashed line shows nominal value)
1.8.4 Corpus Effect
We used the same word-frequency list as Silfverberg et al. [8]. To test for a possible "corpus effect" we also generated predictions with three other word-frequency lists. The first is a much larger list from the British National Corpus that inludes numerous additional low-frequency words. The second is a word-frequency list derived from the Brown Corpus (available from numerous on-line sites). The third is a word-frequency list derived from a set of 500 phrases constructed in-house for our text entry evaluations. These lists are available from the first author upon request. The results are given in Figure 16.
| Corpus | Unique Words | Total Frequencies | WPM Prediction | % of Nominal |
|---|---|---|---|---|
| BNC1 | 9022 | 67,962,112 | 60.74* | - |
| BNC2 | 64,588 | 90,563,847 | 60.21 | 99.1% |
| Brown | 41,532 | 997,552 | 60.18 | 99.1% |
| Phrases | 1163 | 2712 | 59.81 | 98.5% |
| * Nominal value | ||||
1.8.5 SPACE Key Policy
Our nominal prediction assumes a specific policy on SPACE key usage; namely, that the user always presses the SPACE key with the alternate thumb from that used for the last letter in a word. Again, it is not clear that this will occur in practice. And so, we also generated word-per-minute predictions for the two other SPACE key policies described earlier. The results are shown in Figure 17.
| SPACE Key Policy | WPM Prediction | % of Nominal |
|---|---|---|
| Alternate thumb | 60.74* | - |
| Left thumb | 49.92 | 82.19% |
| Right thumb | 56.54 | 93.09% |
| * Nominal value | ||
The predictions in Figure 17 are for the Sharp EL-6810 keyboard which includes a centrally located SPACE key (see Figure 2a). If the SPACE key is offset to the left or right, then the effect of SPACE key policy may be different. For example, the keyboards on the Motorola PageWriter 2000 two-way pager (Figure 2b) and the Nokia 5510 mobile phone (Figure 2d) position the SPACE key to the left of centre. The effect of SPACE key positioning and SPACE key policy are the focus of continuing work in modeling two-thumb text entry.
1.9 Conclusions
This paper presents a model for two-thumb text entry on mobile keyboards. We have provided a detailed behavioural description of the interaction as well as a predicted rate for English text entry. Our prediction of 60.74 wpm is based solely on the linguistic and motor component of the interaction; thus, it is a peak rate for expert users.
Our model's prediction is relatively stable. In a sensitivity analysis, we examined the effect of changes in the various components and parameters that influence the predictions. We generated new predictions after changing corpora, assumed key widths (accounting for thumb width), the minimum time between keypresses by alternate thumbs, and slope coefficients in the movement time prediction equations. In most cases, the predicted text entry rate changed by less than 10%.
A change is text entry throughput of about 7-18% is expected if the user adopts a non-preferential SPACE key policy, such as always using the left or right thumb to press the SPACE key. This expectation is coincident with a centrally located SPACE key. The effect may be somewhat different for other keyboard geometries.
Further work includes building the Fitts' law models for two-thumb text entry, directly observing thumb-to-key assignments and SPACE key policies with users, and testing users on two-thumb text entry tasks with representative keyboards.
References
| [1] | Card, S. K., Moran, T. P., and Newell, A.
The psychology of human-computer interaction,
Hillsdale, NJ: Lawrence Erlbaum, 1983.
|
| [2] | Drury, C. G., and Hoffmann, E. R.
A model for movement time on data-entry keyboards,
Ergonomics 35 (1992), 129-147.
|
| [3] | Kinkead, R.
Typing speeds, keying rates, and optimized keyboard layouts,
Proc of the 19th Annual Meeting of the Human Factors Society.
Santa Monica: Human Factors Society, 1975, 159-161.
|
| [4] | MacKenzie, I. S., and Buxton, W.
Extending Fitts' law to two-dimensional tasks,
Proc of CHI '92.
New York: ACM, 1992, 219-226.
|
| [5] | MacKenzie, I. S., Kober, H., Smith, D., Jones, T., and Skepner, E.
LetterWise: Prefix-based disambiguation for mobile text input,
Proc of UIST 2001.
New York: ACM, 2001, 111-120.
|
| [6] | MacKenzie, I. S., and Zhang, S. X.
The design and evaluation of a high-performance soft keyboard,
Proc of CHI '99.
New York: ACM, 1999, 25-31.
|
| [7] | MacKenzie, I. S., Zhang, S. X., and Soukoreff, R. W.
Text entry using soft keyboards,
Behaviour & Information Technology 18
(1999), 235-244.
|
| [8] | Silfverberg, M., MacKenzie, I. S., and Korhonen, P.
Predicting text entry speed on mobile phones,
Proc of CHI 2000.
New York: ACM, 2000, 9-16.
|
| [9] | Soukoreff, W., and MacKenzie, I. S.
Theoretical upper and lower bounds on typing speeds using a stylus and soft keyboard,
Behaviour & Information Technology 14
(1995), 370-379.
|
| [10] | Zhai, S., Hunter, M., and Smith, B. A.
The Metropolis keyboard: An exploration of quantitative techniques for graphical keyboard design,
Proc of UIST 2000.
New York: ACM, 2000, 119-128.
|