PHYSICS OF THE SPACE ENVIRONMENT

PHYS/EATS 3280

Notes Set 4

The Upper Atmosphere (continued)

Divisions based on Ionisation

When the sun's short wavelength ultraviolet radiation is absorbed in the upper atmosphere by the various constituent gases, ionization may occur and if the density is low enough the electrons released may remain free. These processes lead to the creation of ionospheric layers.

The ionosphere begins at about 70 km and shows a maximum electron density of ~ 8 x 10⁵ electrons cm^-3 at around 300 km altitude. The properties of the ionosphere will be discussed later.

The ionosphere is primarily produced as a result of the interaction of solar radiation with the neutral atmospheric constituents. Therefore, in order to understand the ionosphere we need to look at how solar radiation is absorbed by upper atmospheric constituents.

The Solar Spectrum

As has already been indicated the temperature structure of the atmosphere is also influenced by the absorption of solar radiation, e.g., the absorption of UV (200-300 nm) radiation by ozone in the stratosphere causes heating and leads to the temperature increasing with height. Similarly, the absorption of shorter wavelength UV in the thermosphere leads to heating in that region.

Most of the solar radiation comes from the layer in the sun's atmosphere known as the photosphere i.e. its visible surface. This layer in the sun has a temperature of around 5900 K and the radiation can be approximated by a blackbody curve with this temperature.

A blackbody curve is a good approximation to the solar irradiance at the top of the atmosphere as illustrated by Fig. 4.1 for the wavelength region from 300 nm out to several mm. By the time the radiation reaches the Earth's surface scattering and absorption have modified the spectrum considerably.

Figure 4.1: The solar irradiance at the top of the atmosphere and at sea level.

At wavelengths below a few hundred nm the radiation comes from the outer regions of the sun's atmosphere – the chromosphere and the corona - and it can vary in intensity by several orders of magnitude over a solar cycle.

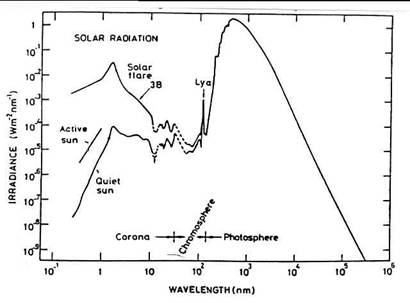
Figure 4.2 Spectral distribution of the solar irradiance and it variation with solar activity. The logarithmic representation emphasizes the contribution of x-rays and extreme ultraviolet radiation.

The short-wave radiation is absorbed in the thermosphere and its strong variation is responsible for the large changes in thermospheric and exospheric temperatures over a complete solar cycle.

Absorption of radiation

The extent to which a particular gas will absorb radiation at a specified wavelength ‘l’ is described by the absorption coefficient ‘k_l’ at that wavelength – a small absorption coefficient implies weak absorption and a large coefficient indicates strong absorption.

If we consider a beam of radiation with intensity I^o entering a column of gas with density r (kg m^-3) the transmitted intensity at point l will be given (according to the Beer-Lambert Law) by

I(l) = I^o exp(-kr l)

where k is the mass absorption coefficient in m² kg^-1.

The quantity kr l is known as the optical depth over the transmission path.

The transmitted intensity can also be expressed as

I(l) = I^o exp(-sn l)

Where n is the absorber number density in molecules cm^-3, l is the path in cm and s is known as the absorption cross section in units of cm² molecule^-1.

The mass absorption coefficient ‘k’ can be readily converted to the equivalent absorption cross section ‘s’ using s = k x 10⁴ x M/Av where M is the molecular weight of the absorber in kg mole^-1 and Av is Avogadro's number = 6.022 x 10²³ particles mole^-1.

Absorption of Radiation in the Atmosphere -The Chapman Function.

The manner in which incoming solar radiation is absorbed by the atmosphere, and the way in which the absorbed solar energy is deposited, is described by the Chapman Function. If the radiation is monochromatic and the absorption cross-section can be considered to be independent of height then in a uniformed atmosphere the incoming solar beam intensity would merely decay exponentially with increasing depth of penetration as shown by curve ‘B’ in Figure 4.3. However, in the real atmosphere the density of most absorbers increases with penetration depth and the intensity of the radiation will therefore fall slowly at first and then more rapidly as the atmospheric absorber density increases. This is illustrated by curve ‘C’ in Figure 4.3

Figure 4.3: Absorption of radiation in an atmosphere. Curve A shows how the denity varies with height h or depth l; Curve B shows how the intensity varies in an atmosphere with constant density; Curve C shows how the intensity varies in an isothermal atmosphere where the density varies as in curve A. The maximum absorption for curve C occurs at point D with height h_m.

The exact manner in which incoming solar radiation is absorbed by the atmosphere, and its energy deposited, may be modeled using Chapman theory.

This theory makes three basic assumptions:

(1) It assumes a ‘flat Earth’

(2) It considers radiation absorbed by a single species at a single wavelength first and builds up

(3) It assumes that the density of the absorbing species may be represented by the simple scale height relationship : n_i(z)=n_i(0)exp(-z/H_i)