The main purpose of this Chapter is to introduce safety first models. The Chapter also demonstrates measures of risk other than the variance which can be utilized to build an "efficient frontier" with respect to these measures. These types of models are not for portfolio management and are not induced by equilibrium arguments like the CAPM.
The problem of portfolio choice or management falls into the general category of decision under uncertainty. Faced with a decision in an uncertain environment, in most cases, the decision is a solution to an optimization problem, albeit with some parameters that are random variables. Such optimization problems are classified as stochastic programming.
Consider an investor that would like to “maximize the return" on his/her portfolio. Since the return is a random variable “maximize the return" is not well defined, as it is a realization of random variables. By choosing a portfolio, an investor can of course affect the realization of the return, its volatility (variance) or the probability that a return above a certain value will be realized. However, by the nature of the problem at hand the return is a random variable and thus the phrase “maximize the return" literally has no meaning.
In the CAPM, the portfolio decision problem is formulated by adapting the variance (standard deviation) as a measure of risk. The set of portfolio(s) for which the expected value of the return is maximized, for a given variance, is identified, and a portfolio is chosen based on the trade off between the measure of risk and the expected return. Hence the optimization problem which is solved in order to choose a portfolio is defined in terms of deterministic parameters: the expected return and variance, which are functions of the portfolios.
The types of models we surveyed here, some of which were developed prior to the CAPM, are induced by the different philosophies (concepts) of converting the stochastic problem into a meaningful deterministic optimization. In these models the risk is not captured directly by the variance but rather by a constraint of the type mentioned above, e.g., constraining the probability of achieving a return below a certain level. For these reasons these methods are commonly referred to as safety first methods. In what follows, we investigate three different methods in this category and we will realize that there is an implicit but intimate relation between these methods and the CAPM.
We continue the analysis based on the assumption that the returns are normally distributed. The results obtained can be generalized and shown to be an approximation for other distributions based on Tchebyshev's inequality. Thus we assume that there are 
securities in the market and that the joint distribution of the return on the securities, 
follows the multinormal distribution with 
and 
We use our usual notation and thus we let:
be the percentage of the portfolio invested in security 
be the rate of return on the portfolio,
or 
be the expected rate of return on the portfolio, and
be the standard deviation of the return on the portfolio.
In order to visualize the feasible set of portfolios for some of the criteria we need to define the following functions:
| > | ExpPortS:=(X::list,mu::list)->sum(X[i]*mu[i],i=1..nops(X)): |
| > | VarPortS:=(X::list,Sigma::listlist)->sum(sum(X[i]*X[j]*Sigma[i][j],i=1..nops(X)),j=1..nops(X)): |
6.1 Roy's Criterion
Roy's Criterion is obtained by converting the maximization of the "return", to a deterministic problem in which a certain return level, 
is given. The portfolio chosen is the one that minimizes the probability that the return will be below 
. In his original paper Roy explained the philosophy behind his method as being related to a catastrophe that one would like to insure against. A person might assess that at least a level of 
is needed for him/her to survive. Hence their objective is to minimize the probability that the return will be less than 
. Roy also motivates his method claiming that such an objective is practical and understood to investors rather than the concept of a utility function and the maximization of expected utility. Based on Roy's criterion the optimal portfolio is the solution to the following optimization problem:
s.t 
where; 
stands for the probability and, if short sales are not allowed we add the constraint
, for 
Since
this probability will be minimized if 
will be minimized.
The same objective will be obtained by solving
s.t 
or equivalently
s.t 
.
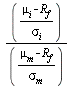
The expression 
= 
should be familiar. It is the excess return per unit of risk. In this case the excess return is measured with respect to 
and the risk is measured by the 
of the portfolio. Given our assumption of the normal distribution, 
and thus the probability of obtaining a return less than 
is determined by 
and 
.
We used the notation of 
instead of 
as we would like to compare it to the CAPM soon. We should note however that, while suppressed, the direct variables of the optimization problems are the holding of each stock in the portfolio, i.e., 
and not 
and 
. The values of 
and 
are consequences of the 
’s. Nevertheless the presentation in terms of 
and 
facilitates the compression to the CAPM and efficient frontiers.
We already know that given 
there may be many portfolios with the same 
but with different 
. Hence we can write the objective function of our optimization equivalently as if the optimization is done in two phases as below:
s.t. 
.
First for each given 
, 
is chosen so as to maximize 
and thus it is clear that the smallest possible 
will be chosen. In the second phase the 
and consequently 
for which 
is the largest is chosen. This presentation makes it clear that the optimal portfolio will correspond to an efficient portfolio since the 
that corresponds to the optimal 
is the smallest possible.
The optimization problems above have the same structure of the problem solved to determine the market portfolio under the CAPM where short sales are allowed. This observation reinforces our conclusion that in a market without a risk-free asset Roy’s criterion will point to a portfolio that is an efficient portfolio, as defined in the CAPM. In our formulation here, 
plays the role of the risk-free rate in the CAPM.
Furthermore, it shows that if Roy's criterion is applied to a market without a risk-free asset, the chosen portfolio is the market portfolio under the CAPM in a market with a risk-free asset where the risk-free rate equals 
. The geometric interpretation is therefore also the same as in the CAPM. In the (
) plane, the value of the objective function 
equals 
if 
or 
. 
will be maximized by choosing the highest 
for which there exists an admissible portfolio satisfying
.
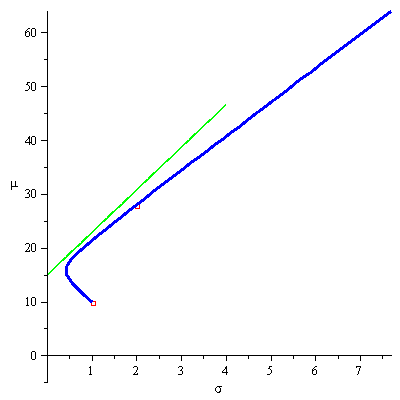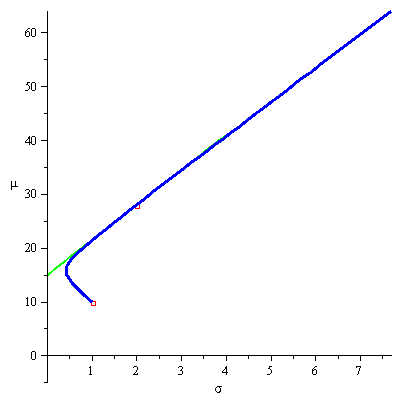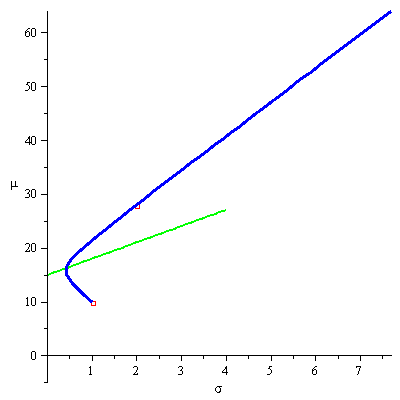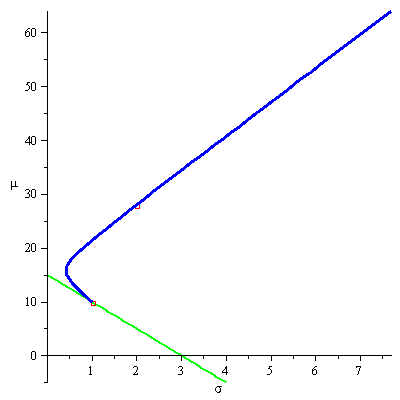
Thus, given 
, we are looking for the highest 
, the slope of the line 
, for which the line has a point in common with the efficient frontier. The optimal 
will thus be the slope of a line that crosses the 
axes (Y-axes) at 
and is tangent to the efficient frontier at a point where the slope of the efficient frontier is 
. The animation below demonstrates this process for 
and an efficient frontier that is built from two portfolios (
)
and 
.
| > | Prim:=plot([[1,10],[2,28]],style=point,symbol=box,thickness=5,colour=red): |
| > | Shortr5:=plot([sqrt(VarPortS([x,1-x],[[1,-0.8*2],[-0.8*2,4]])),ExpPortS([x,1-x],[10,28]),x=-2..1],thickness=3,colour=blue): |
| > | Anil:=plots[animate](15+v*(ExpPortS([x,1-x],[10,28])-15)/sqrt(VarPortS([x,1-x],[[1,0.5*2],[0.5*2,4]])),v=0..4,x=-.5..1,color=green,thickness=2): |
| > | plots[display](Prim,Anil,Shortr5,labelfont=[SYMBOL],labels=[s,m]); |
 |
| > |
From the CAPM we also know that the efficient frontier viewed as a function, 
), is a concave function in 
From the geometry we know that the larger 
is, the larger is 
, the coordinate of the tangency point, and due to the concavity, the smaller the slope is. Hence the larger
is, the smaller is the optimal probability that we can obtain for the portfolio return not to be below 
, which of course makes sense intuitively. Furthermore the larger 
is the larger the 
coordinate of the optimal portfolio, and the larger 
the riskier the portfolio.
Roy does not intend his model to be used as related to the risk attitude of the investor, but rather as minimizing the probability of a catastrophe. The risk the investor is willing to take is communicated by the level of 
Seemingly one may think that the larger 
is the more risk averse the investor is, as the investor would like to minimize the probability of obtaining a return less than 
However, taking a second look at this issue one realizes that to obtain a larger return 
the larger the risk one would need to take to obtain this return. Hence, as our analysis indicated above, the larger 
is the riskier the optimal portfolio is.
If a risk-free rate exists, the efficient frontier is the CML. In this case it is easy to verify that if 
then by choosing the optimal portfolio to be the risk-free rate, the probability of achieving a return less than 
is minimized (it is zero). However if 
the optimization problems defined above are unbounded and hence produce no optimal portfolio.
Given the above, it might be interesting to point out the following facts which shed some further light on the connection between this criteria and the CAPM. We see now that in a market where a risk-free rate exists, the criteria is meaningful only if 
is the risk-free rate. In this case of course the optimal portfolio is composed of only the risk-free asset since for this portfolio the probability of a return less than the risk-free is nil.
However, what will the optimal portfolio be under this criteria when 
is the risk-free rate and there is an additional constraint requiring the portfolio to also include risky securities. The analysis above shows that an optimal portfolio will be the market portfolio. This is because the portfolio for which the probability of receiving a return less than 
is the one which maximizes the slope of the line connecting 
and
. This is exactly how we find the market portfolio. Hence in the CAPM there is another characterization of the market portfolio – a portfolio that does not include only the risk-free asset for which the probability of obtaining a return less than the risk-free rate is minimized.
Furthermore since the probability of obtaining a return less than 
is in one to one correspondence with the slope of the line connecting 
and
, the probability of receiving a return less than the risk-free rate is the same (and the least possible excluding the risk-free rate portfolio) for all portfolios on the efficient frontier – the CML.
Thus there is another characterization of the efficient frontier. The efficient frontier in a market with a risk-free rate is composed of the risk-free rate and all the portfolios for which the probability of receiving a return less than the risk-free rate is minimized. We already mentioned that using Roy’s criteria in a market with a risk-free asset is meaningful only if 
is chosen to be the risk-free asset. In that case however Roy’s criterion cannot be used as a selection criteria for the risky portfolios since all risky portfolios on the CML have exactly the same probability of yielding a return less than the risk-free rate (which is the minimum possible for a risky portfolio) and the risk-free rate obviously has a zero probability for that event.
This point of view also sheds some new light on Sharpe's ratio of the portfolio 
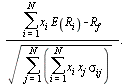
Commonly it is interpreted as the reward for the risk taken i.e., as excess rate of return over the risk free rate per unit of standard deviation of the portfolio. Thus the larger the ratio the better the portfolio since its risk reward trade-off is larger. It can also be interpreted in view of the probability that this portfolio will generate a rate of return less than the risk-free rate. The larger the ratio the smaller this probability is.
We can also interpret the SML in light of the above. The SML stipulates that for each asset (or portfolio) 
,
or since
that
However since 
we can also write it as
or as
which implies 
There is a one-to-one correspondence between 
and 
for each security 
, such that the larger 
the smaller 
. Recall that 
is the Sharpe ratio, or the slope of the lines connecting 
to 
and that the market portfolio as well as each security on the efficient frontier minimizes the probability of obtaining a return less than the risk-free rate. Hence 
indicates a relation between the probability that the market rate of return will be less than the risk-free rate and the probability that the rate of return of security 
is less than the risk-free rate. Consequently, for all securities on the efficient frontier 
This of course can be obtained from first principles since an efficient portfolio is a linear combination of the market portfolio and the risk-free rate. Thus in the CAPM, if 
the probability of security 
having a return less than the risk-free rate is larger than the probability of the same event happening for the market portfolio. Alternatively, 
can be interpreted as the ratio between the Sharpe ratios of security 
to the market portfolio.
This connection of the efficient frontier and the SML, to the probability of obtaining a rate of return less than the risk-free rate, to the best of our knowledge, is not mentioned in the literature dealing with the CAPM. The reason might be due to the fact that Roy's criteria was developed in the early 1950's while the CAPM was not developed until the late 1960's. After the development of the CAPM there was less motivation to re-visit the safety first models which were not, and still are not, very popular with academics.